8 queen
8 queenパズル
チェスのクイーンを8x8のチェス盤に8個、互いに取られないように配置する
パズル。
クイーンは、
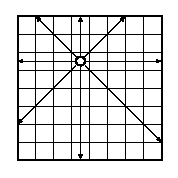
のように八方に動ける。動ける場所に他のクイーンがないような配置とは、
例えば
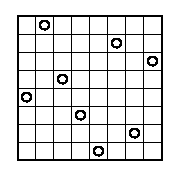
のようなものである。
このような配置は、全部で92通り、回転や裏返しを除くと12通り存在する。
Javaアプレット
ソースはここ。
8 queenパズルを解く
定式化
各列に一つしかクイーンを置けず、また必ず一つクイーンを
おくのは明らかなので、その位置を0〜7の数値で表すと、盤面の状態は
8個の数値で表せる。例えば上の盤面は、
(4 0 3 5 7 1 6 2)
という数値で表せる。これをboard[i]という配列に格納すると、
問題は、
- 全ての i != j について、board[i] != board[j]
- 全ての i != j について、i - board[i] != j - board[j]
- 全ての i != j について、i + board[i] != j + board[j]
を満たすような数字の組を求める問題と見倣せる。
解法
これをいきなり解くのは難しいので、問題を分割する。
すなわち、
- 8queenの全解を出力する関数
- 1列目が固定された状態で、2列目以降を考えて全解を出力する関数
- 1,2列目が固定された状態で、3列目以降を考えて全解を出力する関数
- 1,2,3列目が固定された状態で、4列目以降を考えて全解を出力する関数
- ...
- 1〜7列目が固定された状態で、8列目を考えて全解を出力する関数
のような関数群を用意したと考える。このとき、最後の関数は
簡単なものになろう。n番目の関数は、n+1番目の関数がちゃんと動くならば、
n列目を固定してn+1番目の関数を呼ぶ操作をn列目の全ての可能性について
繰り返せば良い。
再帰呼出し
上のアルゴリズムを実装するには、上記8個の関数を書けばよい
(queen0.c)が、
これを見るとほとんど同じような関数ばかりが並んでいることが分かる。
このような書き方ではバグが混入しやすいし、何よりも8クイーンでなく
Nクイーンを解くようなプログラムを書くことが出来ない。
そこで、全て一つの関数で書いて、引数でその関数が何番目の関数かを
指定することにする。
こう書いたものが、
queen1.c
である。極めて単純になり、かつNクイーンへの拡張も容易になったことが
分かるであろう。
このプログラムは、典型的な「バックトラック法」である。
高速化
上のプログラムで最も時間がかかっていると思われる場所は、
二重ループになっている
for (j=0; j < n; j++) {
if (board[j] == i) goto label;
if (j - board[j] == n - i) goto label;
if (j + board[j] == n + i) goto label;
}
の部分だと思われる。ここの部分を表を引くことによって高速化したものが
queen2.c
である。実行時間を比較すると、
| 盤面の大きさ |
queen1.c |
queen2.c |
| 10 |
0.247 |
0.088 |
| 11 |
1.407 |
0.373 |
| 12 |
8.585 |
2.116 |
| 13 |
54.092 |
11.951 |
となる。(MMX Pentium 166MHz + FreeBSD)
8 queen
/ kashi@mn.waseda.ac.jp


