数独
数独パズル
数独は、ナンバープレイスとも呼ばれる。例えば、
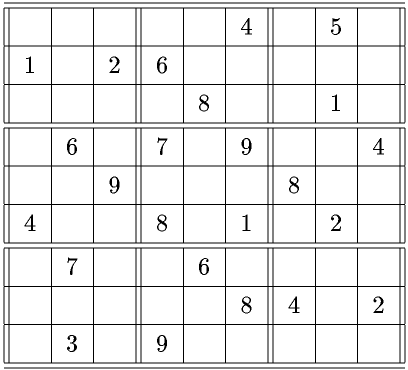
のような9×9の桝目に、
- 同じ行
- 同じ列
- 二重線で仕切られた3×3の小ブロック
に同じ数字が重複しない用に空白に1〜9の数字を当てはめるパズルである。
雑誌等の問題では大抵は解が唯一になるように初期状態が設定されている。
慣れないと結構解くのは難しい。
この問題の全ての解を出力するプログラムを書いて欲しい。
上記の問題は比較的易しいが、
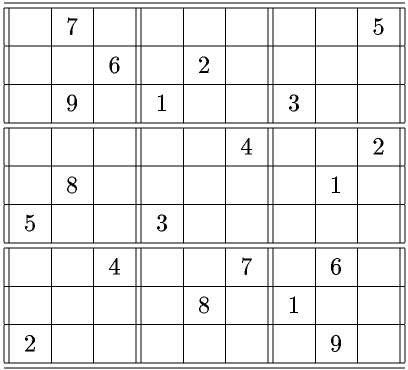
 (宮田 孝富氏作成)
(宮田 孝富氏作成)
は難問である。プログラムは、全て解けるように書くこと。
プログラムについて
以下のプログラム例は、全て
データファイルの書き方
に基づいたデータファイルを読んで、問題の入力を行っている。
この書き方で上記の問題を書くと、
ex1.dat、
ex2.dat
及び
ex3.dat
のようになる。
これは、9×9だけでなく12×12とか16×16の変種の問題も
解けるようにするためだが、レポートはそこまで頑張らなくても
9×9専用で構わない。
解法
本質的には8-queen問題と同じ、バックトラックで解ける問題である。
但し、桝の数が多いため、普通にプログラムを作成したら実行時間が
かかりすぎ、適当に枝刈りを行う必要がある。枝刈りは、
人間が解くときの方法を参考にすると良い方法を思いつくことが多い。
....のはずだったのだが、とりあえず参考のためにと思って
何も考えないバックトラックのプログラムを作って見たら、
上記3問について
とほぼ実用的な時間で解けてしまった(MMX Pentium 166MHz)。
そのプログラムが
sudoku1.c
である。結構長いが、データファイルを読み込む部分が大半で
実際に解いている部分は単純である。
さて、上のプログラムで十分という話もあるが、ここでなるべく再帰に
頼らない高速なプログラムを作る方法を考える。
人間がやるように、全ての桝に入り得る数を列挙しておき、
それを一定のルールに従って消去して可能性を絞り込んでいく方法を考える。
まずは、常識的に次の2つのルールを使うであろう。
- ある桝について、可能性のある数が一つ(a)ならば、その桝を含む
制約ブロックについて、他の桝はaであり得ない。
- ある制約ブロックについて、ある数aを可能性として持つような
桝がただ一つならば、その桝はaである。
この2つのルールを繰り返し適用し、変化しなくなったら仕方がないので
再帰を使うようにしたプログラムが、
sudoku2.c
である。実行時間は、
| 問題1 | 0.010秒 |
| 問題2 | 0.011秒 |
| 問題3 | 0.011秒 |
と極めて高速である。
更に、
- ある制約ブロック内のある数aについて、aを可能性として
持つような桝が2つまたは3つのとき、
その桝を全て含むような他の制約ブロックについて他の桝は
aではあり得ない。
というルール(人間が解くときはよく使う)を組み込んだものが、
sudoku3.c
である。実行時間は、
| 問題1 | 0.014秒 |
| 問題2 | 0.026秒 |
| 問題3 | 0.025秒 |
と逆に少し遅くなってしまった。
ただ、問題1に関してはもはや再帰を使わずに解くようになった。
おまけ
- 数字が入らない部分を指定出来る(正方形以外に対応)
- 最大数より少ない桝からなる制約を許す
コードを加えた
sudoku.c
と、いくつかの変種のサンプル
を付けておく。
ついでに「公開するとしたらこんな感じ?」というドキュメント
sudoku.txtも。
数独
/ kashi@mn.waseda.ac.jp



 (宮田 孝富氏作成)
(宮田 孝富氏作成)